Leitura de dados e gráficos
1. Leitura de dados
Para facilitar a análise sem a necessidade da instalação de quaisquer ferramenta ou ambiente de trabalho, todos os dados utilizados nos exemplos são copiados diretamente do google sheets. Dessa forma também não há necessidade de conectar o ambiente do colab ao drive. Copiando e colando uma tabela simples diretamente na célula, os dados aparecem em CSV no seguinte formato:
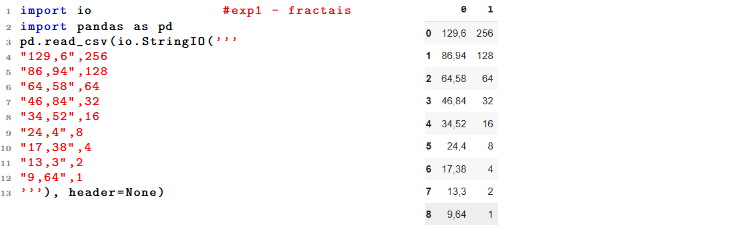
1.1 Tabelas
Nota-se que os dados já aparecem com um código adicional, de forma que ao executa-lo é gerada uma tabela como a mostrada acima. Somente são necessários os dados, a parte entre aspas ('''...'''), definidos no código abaixo. Pelo formato CSV, para ler o arquivo são necessárias as bibliotecas pandas e io, de forma que os dados são traduzidos em arrays, separados por coluna.

Dentro da função do pandas, vista com mais detalhes na aula referente à biblioteca, a função io.StringIO é utilizada para transformar os dados CSV em uma string. Embora já abordado, também vale lembrar que se o decimal estiver indicado com pontos ao invés de virgulas na tabela, basta alterar a variável deicmal da função.
Abaixo, são renomeadas as colunas como X e Y para melhor visualização. Estas são separadas (x e y) e finalmente transformadas em arrays do NumPy ( .values ), para facilitar o uso matemático.
No caso de mais colunas, como em gráficos com incertezas:
1.2 Sequência de dados
No caso de uma histrograma, os os dados podem estar em uma ou multiplas linhas e/ou colunas (independe) de modo a serem traduzidos pelo código abaixo. Segue o exemplo com uma linha única:

Código completo:

Nesse caso, os dados serão trabalhados em formato de lista. A leitura é feita similarmente à versão anterior, excluindo apenas a necessidade do 'sep' pela falta de colunas.
Abaixo são transformados em lista por $.tolist()$, e a função $.flatten()$ garante que independente da disposição dos dados na planilha todos serão lidos como uma sequência única, o que é necessário para a plotagem de um histograma.
1.3 Extra: exclusão de linhas
No caso de haver a nessecidade de exclusão de linhas da tabela por algum critério específico, a operação pode ser realizada com apenas uma linha de código. Seguem abaixo os 2 exemplos mais comuns.
No caso de haverem linhas vazias na tabela, a leitura dos dados CSV devolverá "NaN", que significa ausente. Nesse caso a exclusão pode ser realizada pela segunte função do pandas, já discutida.
No caso de algo ainda mais específico, pode ser realizada uma exclusão manual do dataframe. Segue o exemplo para uma linha de zeros.
Assim, você garante que todos os dados contabilizados serão não nulos. O código mostrado impõe a condição aos dois eixos, mas linhas inteiras podem ser excluídas com condições impostas a apenas um dos eixos. No caso de eliminar todas as linhas de eixo X nulo:
2. Gráficos
2.1 Plotagem dos dados
Para a plotagem de gráficos é importada a biblioteca matplotlib. Usualmente, os gráficos requeridos nas análises são gráficos de dispersão que consideram incertezas, o que objetiva o ajuste de dados a fim da obtenção de parâmetros diversos, a depender do experimento.
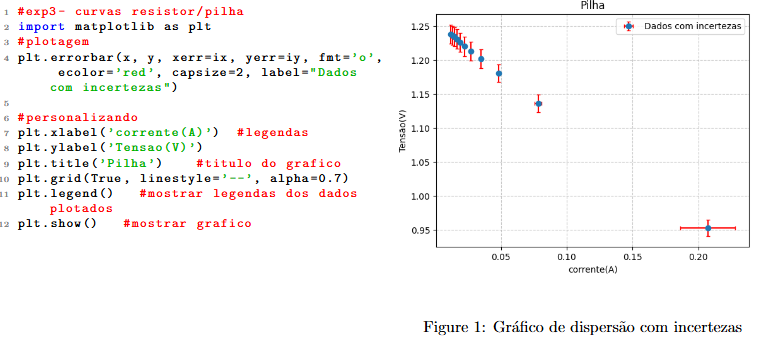
Acima está o código padrão utilizado nas análises exemplo para gráficos desse tipo. A função para a plotagem no caso em que se considera incertezas é plt.errorbar() , e a personalização pode ser complementada, alterando limites do gráfico, eixos e tamanhos de fonte, por exemplo (pode ser encontrado na seção do matplotlib em "bibliotecas base").
No caso de não serem consideradas incertezas a plotagem se dá por:
No caso de histogramas:
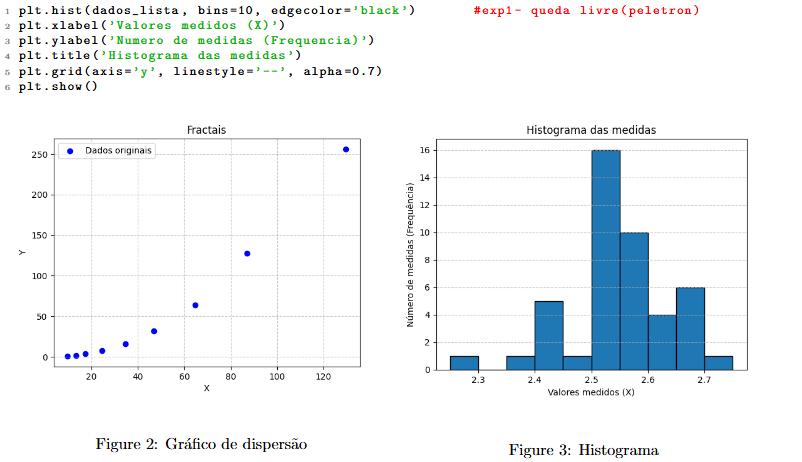
2.2 Ajustes
Nos dois primeiros casos podem ser aplicados ajustes de modelos variados. Segue como exemplo do código utilizado uma aplicação de ajuste linear. Inicialmente, se define a função:
Para realizar o ajuste importamos da biblioteca scipy.optimise a função curve_fit(). Ela conta com a função previamente definida, os arrays referentes a cada eixo, a incerteza associada a y (sigma) e finalmente afirma que os valores de sigma são absolutos e não normalizados. O curve fit define duas variáveis. Primeiramente, os valores ajustados dos parametros, posteriormente reatribuidos às suas referentes incógnitas (nesse caso a e b). Já a covariância define uma matriz que informa como as incertezas no dados afetam os parâmetros ajustados, ou seja, contém as incertezas dos parametros.
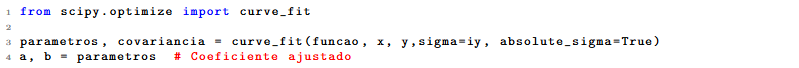
Observação: no caso de não haver incertezas apenas exclua as variaveis sigma e absolute_sigma
Posteriormente deve ser plotada uma curva contínua (plt.plot), em que a função y é aplicada em um array criado com auxílio da função np.linspace (NumPy). Vale lembrar que quanto maior a quantidade de pontos mais suave é a curva gerada.
As incertezas dos parâmetros correspondem às raizes dos elementos da diagonal principal da matriz de covariância.
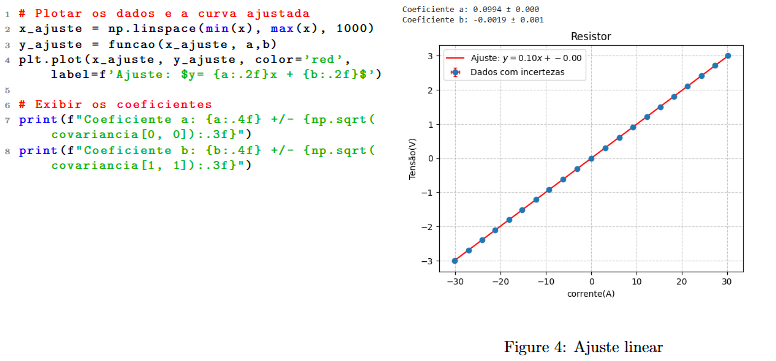
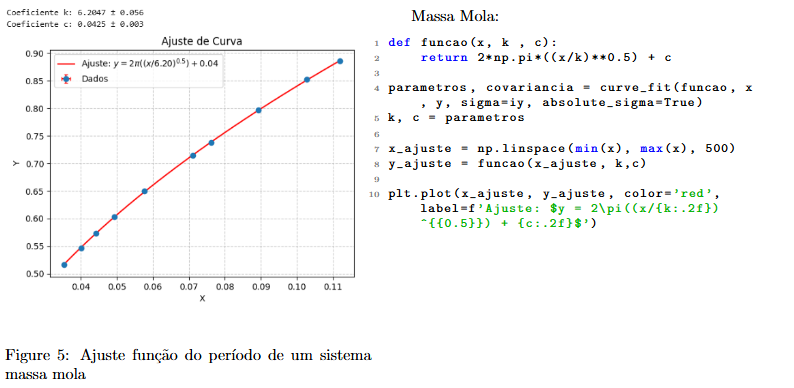
2.2.1 Aplicando para outros modelos
O mesmo código pode ser aplicado para diversos modelos. Além de definir a função correta para ajustar os dados, alterações devem ser feitas nos pontos onde são apresentados os parâmetros (no caso acima a e b). Nos dois pontos indicados devem ser substituidos os parâmetros da função linear apresentada pelos do modelo requerido, assim como no exemplo que segue.
3. Resíduos
Uma importante ferramenta para vizualizar melhor a dispersão de pontos em relação ao ajuste realizado é o gráfico de resíduos. Basicamente, ele aponta a distância entre cada ponto e a curva ajustada no eixo y, o que permite uma análise qualitativa do modelo utilizado naquele caso. Os dois pontos a serem observados é se o intervalo das incertezas cobre a variação dos pontos em torno da curva (como um zoom do gráfico original) e se nesse novo gráfico a dispersão dos pontos aparenta seguir algum padrão. No segundo caso, a dispersão não aleatória geralmente indica que o modelo utilizado está equivocado.
Observação: este recurso não vale no caso de histogramas.
Para ilustrar, ajustamos os mesmos dados com um ajuste linear e um exponencial:
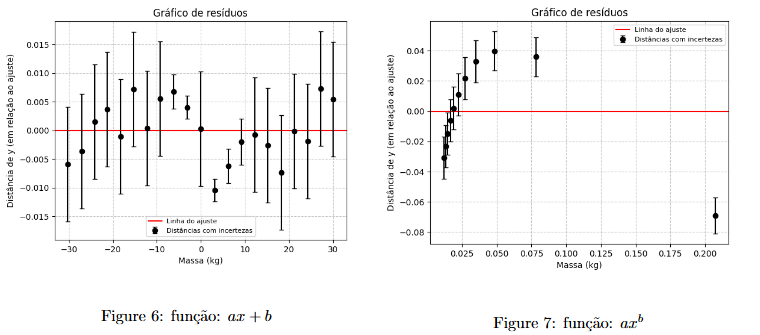
É visível que os pontos estão melhor distribuidos ao redor da linha de ajuste quando se trata do ajuste linear. O segundo gráfico representa um padrão, os pontos formam uma curva que indica que a função exponencial não é a mais adequada neste caso.
A parte da dispersão é plotada como visto anteriormente, a salvo de que a função é aplicada diretamente nos valores de x, não à interesse em criar-se uma cuva contínua. Os valores reais de y são diminuidos dos encontrados e a variação é o que entra como coordenada do eixo y. No caso, o ajuste é representado como uma linha constante no eixo x. Segue o código para uma uma curva linear (Figure 5).

Observação: na primeira linha o underline apenas indica que o parâmetro covariancia (visto anteriomente) nesse caso não apresenta relevância e não será utilizado.
Para plotar a reta no eixo x que representa o ajuste é utilizada a função plt.axhline assim como no exemplo abaixo.

Está incluído também a personalização básica deste gráfico, que seria a mesma figura para as duas plotagens. Em caso deste gráfico estar no mesmo código do gráfico orignal de dados deve ser adicionada a função plt.figure() no início do código.
3.1 Alteração do modelo de ajuste
Nesses casos, como não é necessário reescrever a função que já estará sendo utilizada para a plotagem do gráfico de dados, apenas é necessário se atentar aos pontos onde são apresentados os parâmetros. Os pontos de alteração são similares aos apresentados na aula anterior. Segue um exemplo para o sistema massa mola, também visto no ajuste.

4. Gráfico modelo ATUS
4.1 Plotagem: formatação de imagem
A partir dos princípios discutidos é possível plotar um gráfico único para dados e resíduos, que compartilha o eixo x. A imagem obtida assemelha-se à gerada no ATUS, software utilizado normalmente pelos alunos. Os princípios de plotagem seguem os mesmos, apenas dando maior atenção às dimensões da figura por meio de axes. A função figsize determina o tamanho e o formato da figura, neste caso, quadrada, enquanto fig.add_axes determina as dimensões de cada gráfico em altura, largura e posicionamento. Para As funções referentes ao plot basta substituir plt por ax e o índice do gráfico desejado. Segue abaixo um exemplo dessa adaptação para o experimento da Lei de Own:
5. Plataforma de análise
Como objetivo principal, esse programa é disponibilizado em um Notebook do Google Colab e permite que os alunos baixem uma cópia no próprio computador para que usem durante as disciplinas.
O notebook permite, de forma prática, que o aluno analise os dados coletados e produza gráficos variados, ajustando parâmetros com valor e incerteza associados; além disso, retorna os valores de Chi² e NGL. Assim, esse programa pode ser usado ao invés de softwares, como o Analysis Tool for Undergraduate Students (ATUS) ou o WebRoot, já que possui, a princípio, as mesmas funções.
O arquivo colab contém os códigos completos para gráficos modelo ATUS e histogramas, pode acessa-lo por este link:

