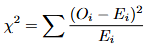1. Qui-quadrado
O qui-quadrado é outro recurso utilizado para analizar a qualidade do ajuste. É uma comparação entre valores obtidos e valores esperados que segue a seguinte fórmula:
Em código, seguindo as definições feitas anteriormente:
Basicamente, quanto mais próximo do número de graus de liberdade (N) for o valor obtido, mais coerente o ajuste realizado. Se o valor para $\chi^2$ for muito maior que N o ajuste não é adequado, caso contrário, o modelo pode estar superajustado ou as incertezas superestimadas.
1.1 Graus de liberdade e valor crítico
Os graus de liberdade são a diferença entre o número de dados obtidos e o número de parâmetros da função de ajuste.
É possível calcular um valor crítico, limite, para o qui-quadrado. Para isso utiliza-se a funçaõ chi2.ppf() da biblioteca scipy.stats . Ela tem como parâmetros N e o nível de significância alfa, geralmente 0.05. Para deixar claro, alfa não apresenta probabilidade de o ajuste estar correto ou não, os 5\% representam o risco de afirmar que o ajuste faz sentido quando ele pode ser só sorte.
OBS: O valor para o qui-quadrado deve ser obtido junto com a plotagem do gráfico pois está relacionado ao ajuste. Logo, o link da plataforma de análise também inclui esta parte.
2. Média e desvio padrão
Normalmente, experimentos em laboratório exigirão uma breve análise comparativa estre os resultados obtidos e esperados, ou valores nominais já conhecidos, a fim de comprovar sua validação. Isso também pode ser feito no python, centralizando assim toda a sua análise e anulando a necessidade da manipulação de tabelas, além de facilitar as contas. Para isso, se fazem necessárias algumas ferramentas, como a média e o desvio padrão. Ambas podem ser calculadas utilizando funções da biblioteca NumPy, podendo ser aplicadas em arrays e listas.
No caso da média, o valor obtido pode ser utilizado como referência, principalmente em conjuntos de dados muito grandes, como aqueles em experimentos com histogramas. Pode ser calculada diretamente por:

Já o desvio padrão, em casos em que o dado de desvio populacional não é conhecido e disponibilizado, normalmente o adequado é calcular o desvio padrão amostral, regido pela seguinte fórmula:

O cálculo pode ser feito diretamente por:

3. Propagação de incertezas
Para encontrar o valor da incerteza de dados obtidos através de funções é necessário propagar a incerteza de cada incógnita. O cálculo segue a fórmula geral abaixo.
É possível definir uma função geral no python que se adapte facilmente a qualquer caso para facilitar a propagação de incertezas. Primeiramente, importe a biblioteca simpy, que permite a mnipulação de incognitas.
Defina a seguinte função:

Esta função recebe os seguintes parâmetros
- func: função em termos das variáveis
- variaveis: lista de variáveis (incógnitas)
- incertezas: lista de incertezas associadas às variáveis (numéricas)
- valores: lista de valores numéricos das variáveis
e retorna o valor da função e sua incerteza propagada. Para ilustrar a aplicação, tomemos como função exemplo:
Devem ser definidas as variáveis, seus valores numéricos e suas respectivas incertezas, e, em seguida, aplicar a função.
OBS: Para calcular outra função basta alterar f e as incógnitas nos 3 pontos onde aparecem x e y.
4. Teste Z
O teste z é usado para verificar se um valor medido está dentro de um intervalo esperado em relação a um valor de referência f_ref. Assumindo que os dados sigam uma distribuição normal e que a incerteza sigma_f já esteja propagada:

O que no python pode ser traduzido como:

Para comprovar a validade usualmente é utilizada como métrica um valor de até 3 vezes a incerteza para o teste Z.