|
 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
Klein Tunnelling and Electron Trapping in Nanometre-Scale Graphene Quantum Dots
BaC6
Buno de Abreu Silva
Tuesday, August 09, 2016
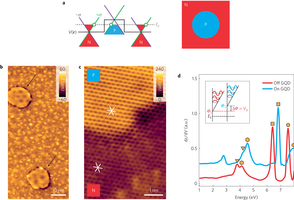
Relativistic fermions that are incident on a high potential barrier can pass through unimped, a striking phenomenon termed the "Klein paradox" in quantum eletrodynamics.
Electrostatic potential barriers in graphene provide a solid-state analogue to realize this phenomenon. Here, we use scanning tunnelling microscopy to directly probe the transmission of electrons through sharp circular potential wells in graphene created by substrate engineering. We find that electrons in this geometry display quasi-bound states where the electron is trapped for a finite time before escaping via Klein tunnelling. We show that the continuum Dirac equation can be successfully used to model the energies and wavefunctions of these quasi-bound states down to atomic dimensions. We demonstrate that by tuning the geometry of the barrier it is possible to trap particular energies and angular momentum states with increased efficiency, showing that atomic-scale electrostatic potentials can be used to engineer quantum transport through graphene
View full text
|
